Model Inversion Attacks on CNN

Imagine you have a mysterious API endpoint that just returns a list of probabilities once you submit an image:

def mock_api_endpoint(model, data):
    # return specific probabilities for a different class
    res = []
    for image in data:
        output = model(image)
        mysterious_classes = # something we don't know yet
        probs = F.softmax(output, dim=1)
        res.append([probs[0][i].item() for i in mysterious_classes])
    return res

For example, when calling this method, we might get somethng like this as an output:

[0.3, 0.4, 0.15, 0.10, 0.05]

Our goal is to find out, what class is actually predicted from our model. Basically, given a function f(x) = y, we want to find f^-1(y) = x. We achieve this by using an encoder-decoder architecture.

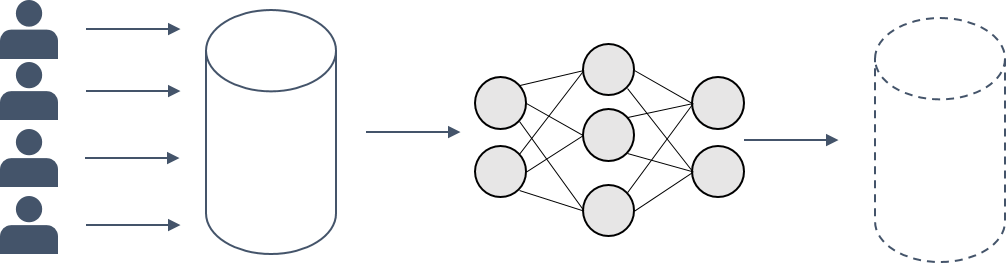
How to invert a given model

Basically, we train our own encoder-decoder architecture to invert the given model. The encoder takes an image as an input and outputs a vector. The decoder takes this vector and outputs an image. The goal is to train the encoder-decoder architecture in a way, that the output of the decoder is as close as possible to the original image. This is done by using a loss function that compares the original image with the output of the decoder. The encoder is trained by backpropagating the loss through the decoder and the encoder. The decoder is trained by backpropagating the loss through the decoder only. Mathematically put, we want to minimize the following loss function:

loss = ||x - D(E(x))||^2

where x is the original image, E is the encoder, D is the decoder and ||.||^2 is the squared L2 norm.

How to find the mysterious classes

We assume we have some knowledge about the initial data used to train the model we want to attack. In our example, we will use the MNIST dataset:

We can define our attack decoder model like this. We need to pay attention that the initial input matches the attacked encoder's output shape. In our case, we obtain a vector of size 5 from the encoder

# Now, we try to invert the model. For each element in the output vector we want to find the input image that maximizes the probability for that class.
# We use gradient ascent to find the input image that maximizes the probability for a given class.
# as forward pass, we only get the api endpoint, so we need to use the model to get the output
import torchsummary

class InvertionModel(nn.Module):
    def __init__(self):
        super(InvertionModel, self).__init__()
        self.layers = nn.Sequential(
            nn.Linear(5, 28 * 28 * 4),
            nn.Sigmoid(),
            nn.Unflatten(1, (4, 28, 28)),
            # scale to 28 x 28
            nn.ConvTranspose2d(
                in_channels=4, out_channels=1, kernel_size=3, stride=1, padding=1, bias=False
            ),
        )

    def forward(self, x):
        x = self.layers(x)
        return x
# define model
invertion_model = InvertionModel()
optimizer = optim.SGD(invertion_model.parameters(), lr=0.01, momentum=0.5)
torchsummary.summary(invertion_model, (5,))

And obtain as output:

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Linear-1                 [-1, 3136]          18,816
           Sigmoid-2                 [-1, 3136]               0
         Unflatten-3            [-1, 4, 28, 28]               0
   ConvTranspose2d-4            [-1, 1, 28, 28]              36
================================================================
Total params: 18,852
Trainable params: 18,852
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.08
Params size (MB): 0.07
Estimated Total Size (MB): 0.15
----------------------------------------------------------------

For visualization purposes, we can define a helper function that plots the output of the decoder. It prints the decoded output that maximizes the probability for a given class. In our case, we get the images for the output [1, 0, 0, 0, 0], ... , [0, 0, 0, 0, 1] (one-hot encoded). We can see that the output of the decoder initially is just noise:

def attack(attack_model):
    images = []
    for idx in range(5):
        target = torch.zeros(5)
        target[idx] = 1.
        with torch.no_grad():
            reconstructed_image = attack_model(target.unsqueeze(0))[0][0]
        images.append(reconstructed_image)
    fig = plt.figure(figsize=(8, 8))
    columns = 5
    rows = 1
    for i in range(1, columns * rows + 1):
        img = images[i-1]
        fig.add_subplot(rows, columns, i)
        plt.tight_layout()
        plt.title("Class " + str(i))
        plt.imshow(img, cmap='gray')


attack(invertion_model)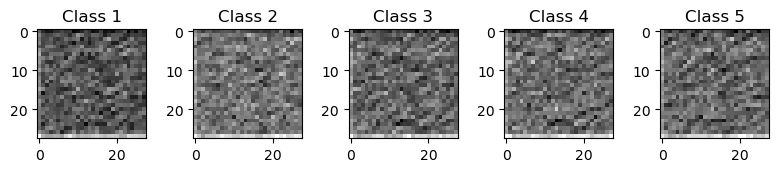

Training the decoder

Now, we actually start training the decoder. As a loss, we define the difference between the output of the decoder and the original image. We use the Adam optimizer to train the decoder. We can see that the output of the decoder gets better and better over time:

attack_optimizer = optim.SGD(invertion_model.parameters(), lr=5e-3, momentum=0.5)


def train_inversion(epochs):
    for epoch in range(epochs):
        for batch_idx, (data, target) in enumerate(inversion_train_loader):
            # get output vector
            output = mock_api_endpoint(model, data.float())
            data.float()
            # zero the parameter gradients
            attack_optimizer.zero_grad()
            # forward + backward + optimize
            output = invertion_model(target)
            if output.shape != data.shape:
                print("Shape mismatch")
                print(output.shape, data.shape)
                break
            loss = ((output - data) ** 2).mean()
            loss.backward()
            attack_optimizer.step()


            if batch_idx % log_interval == 0:
                print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                    epoch, batch_idx * len(data), len(inversion_train_loader.dataset),
                    100. * batch_idx / len(inversion_train_loader), loss.item()))

                train_losses.append(loss.item())
                train_counter.append(
                    (batch_idx * 16) + ((epoch - 1) * len(inversion_train_loader.dataset)))

train_inversion(epochs=3)

We can see that our model trains quite fast. After 3 epochs, we already get a pretty good result: 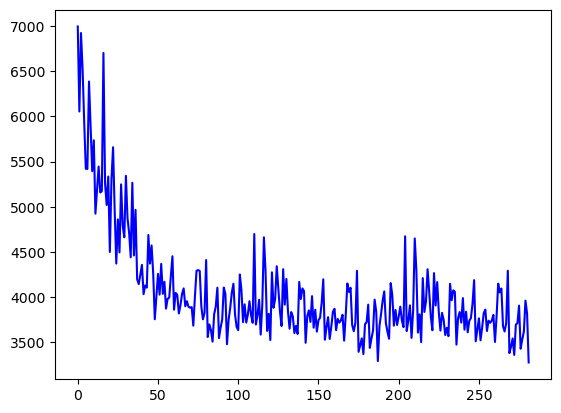Furthermore, our reconstructed images look quite good as well: 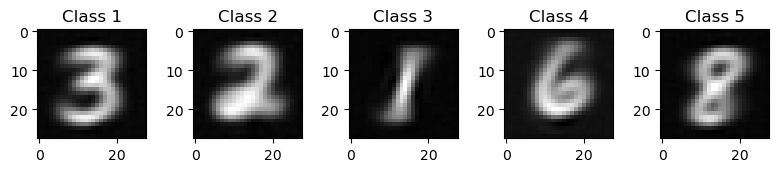It seems like our model outputs 3 2 1 6 8 as the most probable classes that the model gives as output!

Applications

Model Inversion can also be used to reconstruct training images from a model. This can be used to reconstruct training images from a model and thus, potentially, leak sensitive information. For example, if a model is trained on medical data, it might be possible to reconstruct the original images from the model. This can be used to leak sensitive information about the patients. One potential workaround could be to use differential privacy to prevent model inversion attacks.